Для чисел большей разрядности необходимо использовать способ деления, основанный на приведенной ниже вычислительной схеме. Для этого представим необходимо выражение операции деления в следующем виде:

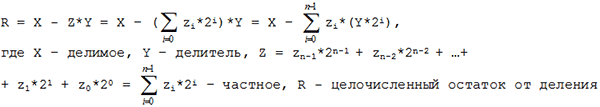
Нахождение частного сводится к отысканию его коэффициентов z_i, которые определяются, согласно формуле, следующим образом: необходимо последовательно сравнивать X с произведениями Y*2ⁱ и если  X > Y*2ⁱ, то в этом случае необходимо произвести вычитание Y*2ⁱ из X, а соответствующий разряд z_i установить в 1; если X < Y*2ⁱ – вычитание пропускается и в этой итерации z_i=0. Эта процедура продолжается до тех пор, пока не останется остаток Ri получаются простым сдвигом Y на i разрядов влево. Аналогично производится деление в любой позиционной системе (метод деления в столбик), но проще всего в двоичной из-за того, что в X может содержаться Y*2ⁱ максимум один раз (на что и указывает единица в соответствующем разряде). Рассмотрим пример деления:

Необходимо обратить внимание на то, что число итераций сравнения должно совпадать с числом значащих разрядов частного (в данном случае n=4 для определения z₀…z₃). Однако разрядность частного заранее никогда не известна и поэтому всегда необходимо знать максимально возможную разрядность результата деления. На практике чаще всего используют вычисления, в которых частное заведомо умещается в 8,16,24, 32 бита (кратно одному байту). При этом нужно использовать 8,16,24,32 итераций сравнения X с Y*2ⁱ, соответственно. С целочисленным остатком R проблем не возникает – его размер ограничен разрядностью Y (R < Y). 

Пусть мы делим uint32_t dividend=179;

на uint32_t B_A=17;

Мы не можем записывать в столбик, как это делали на картинке выше. Поэтому мы будем сдвигать делитель в цикле на 1 разряд влево, пока значение нового делителя tmp не окажется tmp<=dividend && tmp<<1>dividend

Когда будет достигнуто такое tmp, вычтем из dividend значение tmp. Зафиксируем в переменной uint32_t div_part, что делитель был сдвинут на 3: div_part|=(1<<3);

Итак, dividend уже равен  179-(17<<3)=43=0b101011. tmp=17=10001. Распишем dividend -tmp=

101011 -

10001<<1 =

101011 -

100010 =

1001 = 9 - это остаток, то есть дробная часть запишется в виде .(9/17)~0.5294

Сдвиг на 1, потому что
(tmp<<1)<=101011 && (tmp<<1)<<1>101011

Код ниже рассчитывает целую часть числа и дробную с точностью до 2х знаков после запятой. Делятся два 32х разрядных числа. Чтобы делить числа других разрядностей, измените все uint32_t на необходимое (uint8_t для деления байт на байт). Алгоритм ограничен типом uint8_t числа z - количества разрядов, на которое нужно сдвигать. Но так как что-то более ёмкое, чем  uint64_t не предвидится, иметь возможность сдвигать на до 255 разрядов включительно - это даже с запасом.

Скользкий момент dividend=dividend*100;

Здесь может возникнуть переполнения. И следите, чтобы делимое было больше делителя - алгортим написан для такого случая. Иначе придётся переписать вторую часть, начинающуюся как раз с умножения на 100.

uint32_t dividend=179;
                uint32_t B_A=17;
                uint32_t tmp=B_A;
                uint8_t z=0;
                uint32_t div_part=0;
                if (tmp!=0)//на 0 не делят
                    while (dividend>=tmp)
                    {
                        z=0;
                        while ((dividend>=(tmp<<1))&&(z<=sizeof(uint32_t)*8-2)) {//sizeof(uint8_t)*8-2=6, то есть на 6 бит можно сдвигать число влево
                            z++;
                            tmp=tmp<<1;
                        }
                        dividend=dividend-tmp;
                        div_part|=(1<<z);
                        printf("z=%u ",z);
                        tmp=B_A;
                    }
                //сейчас в dividend лежит остаток, тогда ответ: [div_part].[dividend/B_min_A]
                printf("teloe= %u ",div_part);
                
                //теперь будем делить остаток умноженный на 100
                div_part=0;
                dividend=dividend*100;//так как остаток в нашем случае <=2^16-1, то можем умножать на 100 32х битное без переполнения

                tmp=B_A;
                if (tmp!=0)//на 0 не делят
                while (dividend>=tmp)
                {
                    z=0;
                    while ((dividend>=(tmp<<1))&&(z<=sizeof(uint32_t)*8-2)) {
                        z++;
                        tmp=tmp<<1;
                    }
                    dividend=dividend-tmp;
                    div_part|=(1<<z);
                    tmp=B_A;
                }
                //Сейчас в div_part лежат от остатка деления dividend на B_A две цифры
            
                //этот тернарный оператор занимается округлением
                //Пример:div_part равен 25. Это означает, что результат деления dividend на B_A=[целая часть].25
                //Раз сотые доли >=5, в результат дробной части запишем 25 целочисленно делить на 10 +1 = 3
                //div_part= (div_part%10>=5)? div_part/10+1 : div_part/10;
                
                printf(". %u ",div_part);

Про операции с упакованными BCD числами https://studfiles.net/preview/4604039/page:13/